Here at Case Western Reserve University, with fall brings Humans vs. Zombies (HvZ). Loved by some, maligned by others, this campus tradition pits student against student in an epic Nerf-gun-based game of post-apocalyptic tag. While it is not likely for me to participate in events that require running, gunning or going outside, I do like to wonder about the mathematics behind such physical struggle. Because of its root in the spread of zombification, HvZ has the interesting property that it can be modeled using differential equations.

First, for those who have not taken MATH 224/228, a differential equation is an equation that describes the derivative of a function. Differential equations allow mathematicians to compactly describe complex behaviors by tracing how these behaviors change over a certain parameter, usually time (t). Thus, given different starting points, a differential equation can describe the status of certain behavior at any upcoming time. Therefore, given an initial condition, differential equations give us insight into how a system will behave in the future. In our case, differential equations grant us a glance to the final turn out of HvZ.

We will look at HvZ using a differential equation model borrowed from mathematical epidemiology called the SI model. The SI model has two “compartments.” One of them describes individuals who are susceptible (S) to infection from a certain disease, in our case zombification, and the other models those who are infected (I) with that disease, in our case those who have become zombies. If you leave the susceptible compartment then you go into the infected compartment. Once you are infected, you stay infected indefinitely (we do not factor death into our model). These two states, S and I, correspond to a player being a human (H) or a zombie (Z).

To describe the dynamics of our system we make the following assumption: the rate at which humans get infected and become zombies is proportional to the product of the number of humans and the number of zombies. This makes intuitive sense in that the more humans there are, the more likely one of them will unluckily stumble upon a zombie and get infected and vice versa.  Thus we have the differential equation

H’(t) = -aH(t)Z(t)

It follows that the rate of change of zombies must be the negative of this value because we require that if you leave the human compartment you become a zombie. Thus we have the final differential equation system

H’(t) = -aH(t)Z(t)

Z’(t) = aH(t)Z(t)

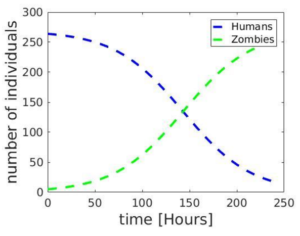
However we have still this pesky constant “a.” For this model we set “a” such that the point where the number of zombies equals the number of humans in our model matches that in the  actual HvZ data from this semester’s HvZ game. After some MATLAB magic we get the following solution: See the graph aside.

If we start with the initial conditions of five zombies and 264 humans, as was the case this semester, our model predicts that there will be about 17 humans still alive at the end of the 10 day period. At the same time, the number of zombies will significantly increase and end up being overwhelmingly higher than human.

While in math the old joke is that “all models are wrong, but some are useful”, this system does provide insight into the dynamics of a game like HvZ. So the next time you see someone running around campus with a nerf gun and a green bandana, relax and remember that, like it or not, it’s just all differential equations.

Writer’s note: A special thanks goes out to the Humans vs. Zombies administrative team for providing me with the data to make this article possible.