One of the joys of living in a dorm is getting woken up at three in the morning by a blaring fire alarm. There is something magical about trudging down 11 flights of stairs, half asleep, only to hear after 20 minutes of standing outside in the cold that someone forgot to put water in their Easy Mac.

Sadly, I am all too familiar with this proud dorm tradition. Living in Clarke Tower, I have seen my share of fire alarms. In fact, according to a university spokesperson, “Since Sept. 1, there has been one ‘full’ fire alarm and five ‘trouble’ alarms at Clarke Tower.” That’s a lot of fire alarms. After one of those woke me up, I got to wondering what the probability of me being blasted out of bed by one of these alarms might be.

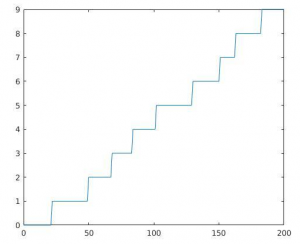
Coincidentally, around the same time as my midnight wake-up-call, a few of my classes were covering something called Poisson processes. You can think of a Poisson process as a way of modeling random arrivals. A good example of a real world phenomena that can be modeled as a Poisson process are the hits on a website. Think about this article, sitting out on observer.case.edu. It starts with zero people having read it, and over time it stays at zero until, as the first person reads it, the “hit count” goes to one. It then stays at one for a while until it jumps to two after a second person reads it, and so on. These website hits, or “arrivals” come at random times in a Poisson process.

We now apply this same idea to the fire alarms in Clarke. Knowing that there have been six fire alarms, summing both the “full” and “trouble” types although there are differences between them. We can say that the “frequency” of fire alarms is six fire alarms per semester, approximately. Ideally we would have more data on this, but here we simply use data from this semester. Now that we have an idea of how often the fire alarm goes off, we can use the Poisson distribution to calculate the probability that, given an eight-hour sleep cycle, you will have a fire alarm go off while you sleep. Because of the properties of the Poisson process this calculation simplifies to

Pr(woken up) = exp(-(6*8))*(6*8)

(where exp is the exponential function). This comes out to be about 7-20. This seems rather low, but when you imagine that many people never get woken up by a fire alarm in their entire college career, and the unlucky few who do usually don’t have it happen more than once, it does not seem entirely unreasonable. That said, as someone who has been woken up by an alarm, it is way too high for comfort.

So the next time you are trudging outside in the wee hours of the morning because someone in your dorm set off the alarms, remember as you stand in the cold Cleveland night that as annoying as fire alarms are, they at least provide the opportunity for some cool calcCWRUlations.